
Математическая статистика
Математическая статистика в психологии
В психологии как науке математическая статистика применяется очень широко. С помощью тех или иных способов, например тестирования, разным особенностям поведения человека сопоставляются числа (шкалируются), и с этими числами уже работают методами математической статистики. После применения этих методов получаются новые данные, которые следует осмыслить.
Без применения математической статистики психология была бы довольно плоской и малоинформативной наукой, основанной на домыслах и спекуляциях (как это, например, имеет место быть в психоанализе). Разумеется, использование математической статистики не является "противоядием" против домыслов и спекуляций, однако предмет рассуждений становится значительно богаче.
Рассмотрим типичный и простой случай использования математической статистики. Допустим, кто-то провел исследование группы школьников. В числе прочих были найдены такие параметры, как экстраверсия-интроверсия и уровень интеллекта. Психолога-исследователя заинтересовало, а как связаны эти параметры между собой. Правда ли, что интроверты в среднем умнее экстравертов? Для этого группу испытуемых (выборку) можно поделить на две подгруппы: экстравертов и интровертов. Далее по каждой подгруппе находится среднее арифметическое по уровню интеллекта. Если, скажем, у интровертов в среднем IQ выше, значит, они умнее экстравертов. Это один подход. Другой может состоять в том, чтобы разделить испытуемых на подгруппу с высоким IQ (более 100) и низким (менее 100), а потом посчитать среднее по экстраверсии-интроверсии в каждой группе. Третий подход может состоять в том, чтобы вместо деления на подгруппы и высчитывания в них средних задействовать более сложный метод - корреляционный анализ. Все эти три методы по-разному, но покажут одну и ту же связь.
Математическая статистика позволяет делать интересные, иногда удивительные открытия. Продолжим наш гипотетический пример. Предположим, что психолог нашел парадоксальный результат, который противоречит с его прошлым опытом, знаниями. Скажем, он установил, что в одной школе экстраверты умнее интровертов, хотя во всех других школах было наоборот. Почему так? Дотошный психолог может начать свое расследование и установит, что, к примеру, это связано с тем, что в этой школе экстраверты ходят на факультатив по физике (потому что там «заводной учитель») и развивают свой интеллект, а интроверты ходят на факультатив по литературе (потому что там «душевный учитель»), где развивают другие качества своей души. Может ли, например, психоаналитик дойти до такого открытия? Крайне маловероятно.
В психологических исследованиях в расчет берутся не только такие чисто психологические параметры, как, скажем, интеллект, экстравертированность или тревожность. Могут использоваться и такие данные, как возраст, пол, уровень образования, рост, вес, физическая сила, политические взгляды, стаж работы и многое другое. Часто бывает, что именно без таких непсихологических показателей исследования оказываются неполными, малоинформативными. Также часто бывает, что представители других наук (например, социологии или биологии) тоже используют психологические параметры в своих исследованиях.
Математическая статистика позволяет много вещей:

Практические психологи в своей работе обычно ограничиваются нахождением средней арифметической, с разделением на подгруппы (как в примере выше). Ученые-психологи используют самый разнообразный арсенал методов математической статистики. Рассмотрим основные.
Нахождение средней арифметической
Самый банальный и простой метод. Показатели (например, рост испытуемых) складываются, затем делятся на число испытуемых. Несмотря на простоту, метод, конечно, очень информативный и наглядный. Наглядность - важное качество метода для практического психолога. Когда он представляет результаты своих исследований заказчику (например, директору школы), тот далеко не всегда способен понять сущность корреляционного или дисперсионного анализа. Разделение испытуемых на подгруппы по произвольному основанию усиливает потенциал средней арифметической, позволяя закрыть большинство потребностей исследователя.
Нахождение моды и медианы
Предположим, мы обследовали 1000 студентов - измеряли их рост с точностью до сантиметра. Эти данные заносили в таблицу. Если в таблице чаще всего встречается значение, скажем, 172 сантиметра, это и есть мода нашей выборки. Аналогичным, кстати, образом слово "мода" используется и в быту: если в этом сезоне чаще всего можно встретить шапочки красного цвета, значит это мода, хотя на долю этих шапочек может приходиться всего лишь 20 или 30 процентов.
В психологических исследованиях обычно мода находится где-то рядом со средней арифметической. Если мода 172 см, то и средняя будет около того. Чем больше выборка, тем ближе мода и среднее арифметическое.
Далее. Предположим, мы поделили своих студентов на две равные группы: в первой группе 500 низких студентов, во второй группе 500 высоких студентов. Значение роста, которое приходится на 500-го или 501-го студента и есть медиана. Медиана обычно тоже находится рядом со средней арифметической.
Выявление рассеяния значений
Как известно, средняя температура по больнице не так уж важна. И в хорошей больнице, где лечат хорошо, средняя температура может быть 36,6°C; и в плохой может быть такая же: просто у кого-то жар в 40 °C, а кто-то уже умер, и у него 18°C.
Самый простой способ оценить рассеяние выборки - найти ее размах (иначе - разброс). Если в нашей выборке самый низкий студент имеет рост 148 см, а самый высокий 205 см, значит размах выборки составит 205-148=57 см. Это величина важна в первую очередь для того, чтобы оценить, в каких рамках вообще меняется данный параметр.
Далее. Предположим такую ситуацию. Лет через двадцать по прихоти какого-нибудь богатого человека у него появятся дети-клоны. Ещё через двадцать лет они поступят в университет. И будет в университете выборка студентов объемом 1000 человек, из которых 998 имеют рост 177 см, один - 148 см, один - 205 см. По основным параметрам - средней арифметической, моде, медиане, размаху - эта выборка может не отличаться от другой выборки студентов (там будут такие же значения). Но при этом во второй (нормальной) выборке будет какое-то количество студентов с ростом 150-160 см, какое-то с ростом 180-190 см и т.д. Так что же, получается, что с точки зрения математической статистики эти группы одинаковые?
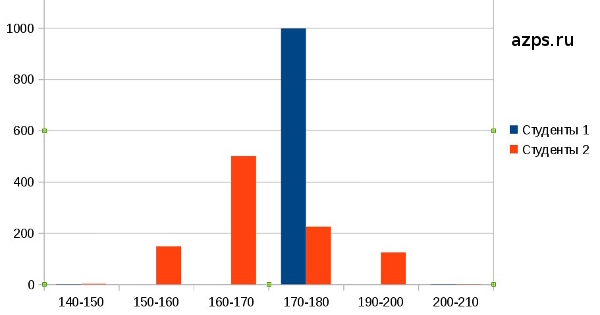
Одного взгляда на этот рисунок достаточно, чтобы понять, что группы различаются по рассеянию значений. Поэтому в статистике есть более точный инструмент для оценки рассеивания - дисперсия. Дисперсию исчисляют так: находят среднее арифметическое, потом для каждого случая находят отклонение от среднего, возводят это значение в квадрат, в конце делят на общее количество случаев. Из значения дисперсии легко получить стандартное отклонение: оно есть квадратный корень из дисперсии. Стандартное отклонение обозначает, что понятно, стандартное отклонение: то есть мера того, насколько в среднем значения вообще отклоняются.
Стандартное отклонение измеряется в тех же самых единицах, что и сам параметр. В первой нашей гипотетической группе, где почти все студенты одинаковы, стандартное отклонение будет крайне малым (менее 1 см). Во второй группе будет значительно больше - сантиметров 10-15. Если нам скажут, что средний рост студентов составляет 175 см при стандартном отклонении 12 см, мы будем знать, что большинство студентов (примерно 2/3) находится в диапазоне от 163 до 187 см.
t-критерий Стьюдента
Предположим, мы решили провести эксперимент такого рода. Мы взяли группу испытуемых. Перед началом эксперимента протестировали их, скажем, на уровень креативности. Далее они целый месяц занимались по часу в день рисованием. В конце эксперимента мы опять проверили их на уровень креативности. Был замечен результат, но довольно малый, и скептики стали нам заявлять, что уровень креативности не повысился, небольшое повышение средней арифметической это всего лишь случайность.Для таких ситуаций придумали разные критерии. Один из них - наиболее популярный - это t-критерий Стьюдента. В числителе у него разница средних арифметических. В знаменателе - корень из суммы квадратов дисперсий (имеется в виду первый и второй случай тестирования). Чем больше разница между средними арифметическими, тем лучше (наш труд не остался напрасным), и чем меньше разброс значений в обоих случаях диагностики, тем тоже лучше: когда разброс значений больше, тогда и случайные колебания тоже больше.
Для применения данного критерия есть существенное ограничение - распределение показателей должно быть близко к так называемому нормальному (колоколообразному).
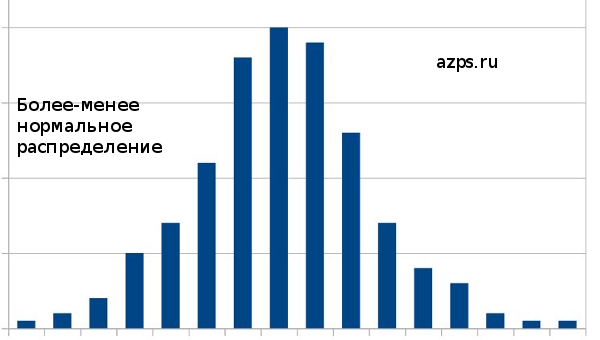
Существуют специальные критерии для определения степени нормальности распределения.
Корреляция
В психологии, как наверное ни в одной другой науке, любят находить коэффициенты корреляции. Существует несколько разных подходов, в том числе и для нормального, и для не нормального распределения. Все они показывают степень зависимости одного параметра от другого. Если один параметр (например, вес человека) сильно зависит от другого параметра (например, рост человека), тогда коэффициент корреляции будет близок к +1. Если зависимость обратная (например, чем человек выше, тем менее ловок он), тогда коэффициент корреляции будет стремиться к -1. Если зависимости нет (скажем, удачливость при игре в карты не зависит от роста человека), тогда коэффициент корреляции будет около 0.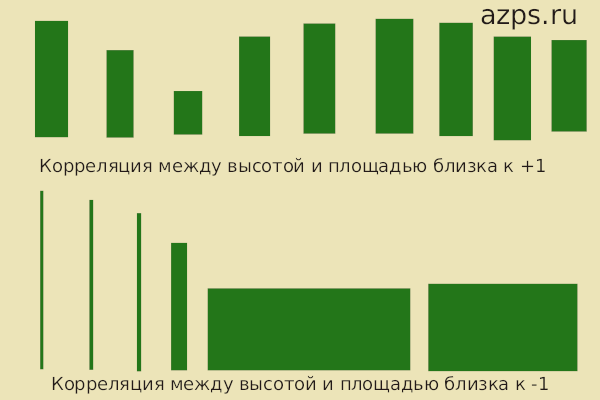
Если взять группу испытуемых, зафиксировать их рост и вес, а потом результаты перенести на двухмерный график, то получится примерно следующая картина, которая свидетельствует о том, что корреляция положительная, примерно на уровне +0.5.
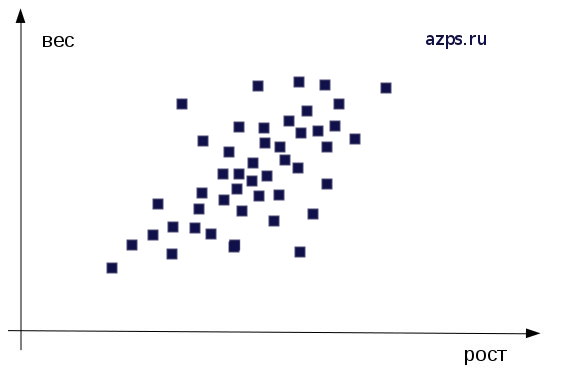
Факторный анализ
Наиболее, пожалуй, таинственный анализ. Некоторая загадочность его объясняется тем, что сам он предназначен для того, чтобы найти новый параметр, который многое объясняет, но при этом непосредственно в ходе эксперимента не исследовался. Как правило, в ходе факторного анализа находятся наиболее влиятельные параметры, от которых зависят более мелкие, частные.Допустим, мы проводили исследование со школьниками. В числе прочих фиксировались следующие параметры: общая успеваемость, успеваемость по точным предметам, успеваемость по гуманитарным предметам, объем кратковременной памяти, объем и распределение внимания, активность мышления, пространственное воображение, общая осведомленность, общительность, тревожность. Если применить корреляционный анализ и составить так называемую матрицу корреляций (где отражена связь каждого параметра с каждым), то можно увидеть, что большинство этих параметров между собой хорошо коррелирует. Исключение составляет последние два, которые с другими связаны слабо. Уже глядя на эту матрицу можно предположить, что за большинством параметров стоит некий один общий (сверх-параметр), который на них на всех влияет. Мы проводим процедуру факторного анализа, и после этого в нашей матрице появляется еще один столбец - столбец без названия. Этот загадочный параметр очень хорошо коррелирует со всеми (кроме общительности и тревожности). После некоторого творческого раздумья психолог приходит к единственно возможной здесь интерпретации - загадочный параметр это есть интеллект. Он и влияет на все остальное, влияние его сильное, хотя и не стопроцентное.
Существуют методы факторного анализа, которые помогают выявить не один, а несколько факторов, которые влияют на другие параметры. Часто так бывает, конечно, что загадочный параметр оказывается не таким уж и загадочным, а полностью совпадает с одним из тех параметров, которые фиксировались. Но иногда бывает и так, что придется долго поломать голову прежде, чем удастся интерпретировать этот секретный фактор.
Факторный анализ применяется в основном учеными для глубокого понимания предмета исследования. При этом следует учитывать, что для точности результата необходимо довольно большое количество испытуемых: желательно, чтобы количество испытуемых в разы превышало количество параметров.
С помощью факторного анализа можно изучать качество психологических тестов. Если взять, например, какой-нибудь личностный опросник с несколькими параметрами, подвергнуть эти параметры факторному анализу, то может всплыть некий странный общий фактор, влияющий на все параметры. Значимого психологического смысла он может не иметь - это просто тенденция испытуемого отвечать так или иначе по формальному признаку (кто-то отвечает вдумчиво, кто-то склонен выбирать первые пункты из вариантов, кто-то последние). Большое влияние этого общего фактора может говорить о недостаточно качественной проработке заданий.
Литература
Ермолаев О. Ю. Математическая статистика для психологов: Учебник. - 2-е изд. испр. - М.: МПСИ, Флинта, 2003. - 336 с.
- Альфа Кронбаха
- Показывает внутреннюю согласованность характеристик, описывающих объект.
- Измерения в психологии
- Процедуры сопоставления каких-либо проявлений психического специальной шкале, представляющей собой некоторое множество позиций, которые поставлены в некоторое соответствие с психологическими элементами. Выделяются следующие шкалы: отношений, интервальная, порядковая и номинальная.
- Интервальная шкала
- (шкала интервалов) метрическая шкала, отображающая как отношения наименований, отношения порядка, так и отношения расстояний между парами объектов.
- Кластерный анализ
- Процедура математической статистики, позволяющая на основе нахождения связи количественных значений нескольких признаков, свойственных каждому объекту (например, испытуемому) какого-либо множества, сгруппировать эти объекты в определенные классы (кластеры).
- Корреляционный анализ
- Статистический метод оценки формы, знака и тесноты связи исследуемых признаков или факторов.
- Латентный анализ
- Метод математической статистики, позволяющий анализировать структуру связей между ненаблюдаемыми переменными, полученными в эксперименте.
- Порядковая шкала
- Метрическая шкала, отображающая отношения эквивалентности и отношение порядка. Каждый элемент по выраженности шкалируемого признака сопоставляется с другими, но без использования единицы измерения.
- Репрезентативность выборки
- Важное понятие для социологии и психологии - соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом.
- Шкала отношений
- Метрическая шкала, в которой возможно лишь преобразование подобия: умножение шкальных значений на константу, выступающей единицей измерения.
См. также
Экспериментальная психология- Артефакт
- Компьютерная томография
- Кривая упражнения
- Методология экспериментальных исследований личности
- Методы изучения речи
- Методы исследования эмоций
- Мысленный эксперимент как объективный метод исследования
- Надежность измерения
- Плетизмография
- ... и другое
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я